[ML] 다변수 함수의 수치미분

일변수 함수의 수치미분과 마찬가지로 아래의 공식을 통하여 다변수 함수의 수치미분 값을 구한다.

( f(x+delta_x) - f(x-delta_x) ) / ( 2 * delta_x )

 

독립 변수가 세개인 f(x,y,z) 의 함수가정. 특정 좌표 (1,2,3) 에서 각 변수에 해당하는 편미분 값

 

(1,2,3)에서 x의 편미분 값 -> 계산 값 a 가정

( f(1+delta, 2, 3) - f(1-delta, 2, 3) ) / (2 * delta)

 

(1,2,3)에서 y의 편미분 값 -> 계산 값 b 가정

( f(1, 2+delta, 3) - f(1, 2-delta, 3) ) / (2 * delta)

 

(1,2,3)에서의 z의 편미분 값 -> 계산 값 c 가정

( f(1, 2, 3+delta) - f(1, 2, 3-delta) ) / (2 * delta)

f'(1,2,3) = (a,b,c) 이 된다.

---

f(x,y) = 2x + 3x^2 + y^2 함수의 (1,2) 좌표에 해당하는 미분값을 계산

(하나도 개선하지 않은 코드로 먼저 작성 후 코드를 개선해 봄)

 

func1 (다변수 함수. 현재는 x,y 두개의 독립변수에 해당하는 함수)

# 인자에 전달된 input_array(특정 좌표 벡터)를 사용하여 다변수 함수 값 계산
def func1(input_array):
    x = input_array[0]
    y = input_array[1]
    return (2 * x) + (3 * x * x) + (y ** 2)

 

함수 테스트 - (1,2) 에 해당하는 함수 값 계산

value = np.array([1.0, 2.0])  # 벡터를 함수의 인자에 전달
print(func1(value))

 

---

derivative ( delta를 이용하여 값을 만든 후 func1함수를 이용하여 편미분을 구하는 함수)

# 넘겨 받은 좌표 값에서 각 독립 변수에 해당하는 편미분 값을 구하는 함수
def derivative(input_array):
    delta = 1e-4
    gradient = np.array([0.0, 0.0])  # 편 미분 값을 담기 위함. 계산 후 return 할 변수

    x = input_array[0] 
    y = input_array[1]  

    # y고정, x의 편미분 구하기
    x_plus_delta = x + delta
    x_minus_delta = x - delta

    f1 = func1(np.array([x_plus_delta, y]))
    f2 = func1(np.array([x_minus_delta, y]))
    gradient[0] = (f1 - f2) / (2 * delta)

    # x고정, y의 편미분 구하기
    y_plus_delta = y + delta
    y_minus_delta = y - delta
    f3 = func1(np.array([x, y_plus_delta]))
    f4 = func1(np.array([x, y_minus_delta]))
    gradient[1] = (f3 - f4) / (2 * delta)

    return gradient


value = np.array([1.0, 2.0])  # (1,2) 좌표 벡터
print(derivative(value))  # f'(1,2) 계산

(x편미분:  2 +6x,  y편미분: 2y) -> (1,2)좌표 -> (8,4)

 

배열을 int32로 넘길경우 함수 내부에 float으로 캐스팅하는 코드가 있어야 한다. 

---

(개선된 코드에 필요한 개념)

 

np.zeros_like - 인자에 전달된 것과 같은 차원에 해당하는 0으로 채워진 넘파이 배열 생성

arr = np.array([1, 2])
print(np.zeros_like(arr))
print()

arr2 = np.array([[1, 2],
                 [3, 4]])
print(np.zeros_like(arr2))

---

numpy 배열은 인덱싱시 튜플을 사용할 수 있다. 

import numpy as np

test = np.array([[1, 2],
                 [3, 4]])

print('test[0][0]: ', test[0][0])
print('test[0,0]: ', test[0, 0])
print('test[(0,0)]: ', test[(0, 0)])  # 인덱싱에 튜플을 사용할 수 있다
tup = (0, 0)
print('test[tup]: ', test[tup])

---

numpy 배열 반복

import numpy as np


def info(obj):
    print('type: ', type(obj))
    print(obj)
    print()


arr = np.array([[1, 2],
                [3, 4]])

print('arr')
print(arr)

it = np.nditer(arr, flags=['multi_index'], op_flags=['readwrite'])

while not it.finished:
    tup = it.multi_index
    print('..........')
    print('tup')
    info(tup)
    print('arr[tup]: ', arr[tup])
    it.iternext()

 

---

(개선된 코드)

각 반복에 각 독립변수 좌표를 임시변수에 저장한 후 

독립변수 좌표 + delta , 독립변수 좌표 - delta의 두 함수 값 계산후 독립변수 편미분 값 계산

def derivative(input_array):
    delta = 1e-4
    gradient = np.zeros_like(input_array)  # [0.0, 0.0]

    it = np.nditer(input_array, flags=['multi_index'], op_flags=['readwrite'])

    while not it.finished:  # 주석 - 첫 반복 내용
        index = it.multi_index  # (0,)
        temp = input_array[index]  # x값 백업

        input_array[index] = temp + delta  # 배열을 x+delta 로 변경
        f1 = func1(input_array)  # 변경된 배열을 통해 f(x+delta, y) 계산

        input_array[index] = temp - delta
        f2 = func1(input_array)  # 변경된 배열을 통해 f(x-delta, y) 계산

        gradient[index] = (f1 - f2) / (2 * delta)

        input_array[index] = temp
        # 배열의 x+delta, x-delta 사용했던 것을 x로 복원 시켜야 다음 독립 변수 y편미분때 
        # x의 고정 좌표 값 사용가능

        it.iternext()  # 다음 반복

    return gradient

 

coordinate = np.array([1.0, 2.0])  # (1,2) 좌표 벡터
gradient = derivative(coordinate)  # f'(1,2) 계산
print(gradient)
print(gradient[0])
print(gradient[1])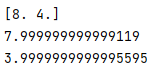

---

이제 다변수 함수를 변경할 경우 func1의 코드만 변경 가능하게 된다.

f = 2x + 3x^2 + y^2 + z^2 + t^2 의  f'(1,1,1,1) 계산

def func1(input_array):
    x = input_array[0]
    y = input_array[1]
    z = input_array[2]
    t = input_array[3]
    return (2 * x) + (3 * x * x) + (y ** 2) + (z ** 2) + (t ** 2)

coordinate = np.array([1.0, 1.0, 1.0, 1.0])
print(derivative(coordinate))

각 편미분 2 + 6x , 2y, 2z, 2t -> f'(1,1,1,1) -> (8,2,2,2)

---

벡터 대신 행렬을 사용하여도 func1 함수만 변경하면 된다.

 

def func1(input_array):
    x = input_array[0, 0]
    y = input_array[0, 1]
    z = input_array[1, 0]
    t = input_array[1, 1]
    return (2 * x) + (3 * x * x) + (y ** 2) + (z ** 2) + (t ** 2)

# 2 x 2 matrix
coordinate = np.array([[1.0, 1.0],
                       [1.0, 1.0]])
print(derivative(coordinate))